Reference: Terziyan V., Social Distance Metric: From Coordinates to
Neighborhoods, International Journal of Geographical
Information Science, 31 (12), 2401-2426, Taylor
& Francis,
2017. (doi: 10.1080/13658816.2017.1367796)
For any two points ![]() and
and ![]() in some data space with metric
in some data space with metric ![]() , we define the “mutual social ranking” function
, we define the “mutual social ranking” function
![]() as follows:
as follows: ![]() , if point
, if point ![]() is the
is the ![]() -th nearest neighbor of the point
-th nearest neighbor of the point ![]() in metric
in metric ![]() ; and
; and ![]() , if
, if ![]() . Similarly:
. Similarly: ![]() , if point
, if point ![]() is the
is the ![]() -th nearest neighbor of the point
-th nearest neighbor of the point ![]() in metric
in metric ![]() . It is evident that
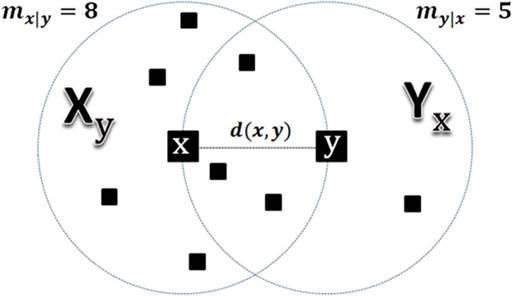
. It is evident that ![]() and
and ![]() are not necessarily equal (see the example of
the mutual social ranking asymmetry in the figure below where the point
are not necessarily equal (see the example of
the mutual social ranking asymmetry in the figure below where the point ![]() for the point
for the point ![]() is
the eighth closest one while the point
is
the eighth closest one while the point ![]() for the point
for the point ![]() is
the fifth closest one).
is
the fifth closest one).
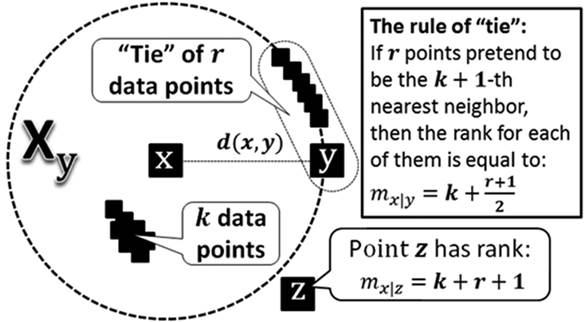
Special case (“rule of tie”): If ![]() points (including point
points (including point ![]() ) pretend to be the
) pretend to be the ![]() -th nearest neighbor of point
-th nearest neighbor of point ![]() , then:
, then: ![]() .
.
Having ![]() and
and ![]() due
to the use of some metric
due
to the use of some metric ![]() , and choosing
, and choosing ![]() , we can compute the Social Distance
, we can compute the Social Distance ![]() between
between
![]() and
and ![]() as
follows:
as
follows:
I.
First
we average ![]() and
and ![]() in
a special way. We compute
the Lehmer mean of
in
a special way. We compute
the Lehmer mean of ![]() and
and ![]() , which is:
, which is:
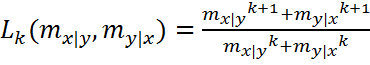 .
.
Notice that this averaging function includes
most of famous means depending on ![]() . E.g., it is equals to Arithmetic
mean for
. E.g., it is equals to Arithmetic
mean for ![]() , and to Contraharmonic mean for
, and to Contraharmonic mean for ![]()
![]() See more cases and details in the referred article.
See more cases and details in the referred article.
II.
Using
the Lehmer mean above, we compute the Social Distance as follows:
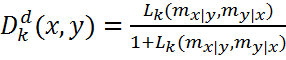 .
.
… and we have
proven it (and several modifications of it) to be a metric suitable for many intelligent
data processing tasks (classification, clustering, etc.) See details in the
article.
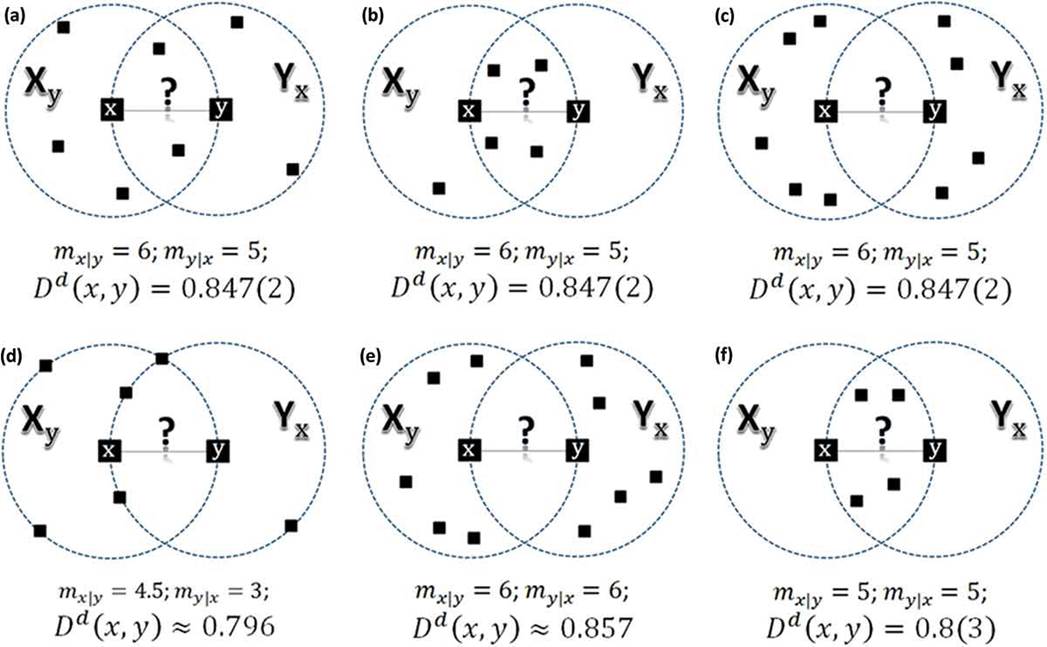
See examples of the Social Distance computing for different
neighborhoods in 2D space for the same pair of data points ![]() and
and ![]() : cases (a)–(c) have different
configuration resulting to the same distance; (d) case with some data points at
the border of the neighborhood (ties); (e) and (f) cases with symmetric
neighborhoods.
: cases (a)–(c) have different
configuration resulting to the same distance; (d) case with some data points at
the border of the neighborhood (ties); (e) and (f) cases with symmetric
neighborhoods.